
See discussions, stats, and author profiles for this publication at. For Q 0, the quantity in the square brackets is equal to 1 and e(Q) then reduces to the Thomas-Fermi dielectric function 4. View ThomasFermimodelofelectronicscreeni.pdf from PHYSICS PHYS 223 at Laikipia University. e(Q) given by (4.159) is also known as the Lindhard dielectric constant 4.69. This additional screening in turn leads to the asymptotic incomplete screening form for the potential: φ(r)≊Ze/ ε 0r, where ε 0 is Z dependent and thus not equal to the bulk dielectric constant associated with the background. In this equation, n is the conduction electron density, Ep the Fermi energy and kp the radius of the Fermi sphere. take in the form of a self-consistent screening field. The partial filling of the conduction band near the point charge gives rise to a Z-dependent screening in addition to that of the usual form due to the background dipole density of the insulator (the latter is treated phenomenologically). Here we have introduced the Thomas-Fermi wavevector: qTF e2m. The induced electron density in the conduction band near the point charge, expressed in terms of the electrostatic potential, is used in forming the Thomas-Fermi equation.
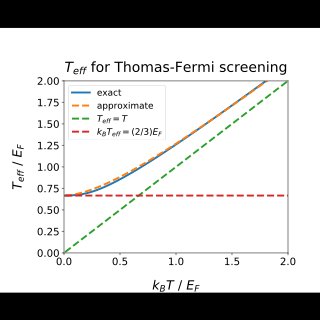
In contrast to the corresponding familiar problem for a metal, the density of states, which enters into the Thomas-Fermi analysis, is here appropriate to a model band structure with two bands and a gap.

The Thomas-Fermi treatment of screening of a point positive charge Ze in a model insulator is developed.


 0 kommentar(er)
0 kommentar(er)
